Aufgaben und Lösungshinweise zum Staatsexamen
Thema 1
- Definieren Sie die Begriffe "lokales Extremum" und "globales Extremum" und formulieren Sie notwendige und hinreichende Kriterien für lokale Extrema reeller Funktionen! Beweisen Sie ein notwendiges Kriterium für lokale Extrema!
- Erläutern Sie zwei unterrichtliche Aktivitäten zur Ermittlung von Extrema bei reellen Funktionen und nennen Sie je ein zugehöriges Lernziel!
- Entwickeln Sie eine Unterrichtseinheit, in der die folgende Aufgabe bearbeitet wird: "Aus einer Kugel soll ein gerader Kreiszylinder maximalen Volumens herausgeschnitten werden."
Thema 2
- Erläutern Sie das Heron-Verfahren zur Bestimmung von Quadratwurzeln! Gehen Sie dabei auch auf dessen geometrische Darstellung ein!
- Erläutern Sie zwei unterrichtliche Aktivitäten, die zur Einführung irrationaler Zahlen geeignet sind!
- Entwickeln Sie eine Unterrichtseinheit zur näherungsweisen Bestimmung der Dezimaldarstellung von irrationalen Quadratwurzeln!
Thema 3
- Formulieren und beweisen Sie den Basiswinkelsatz für gleichschenklige Dreiecke und seine Umkehrung!
- Erläutern Sie drei unterrichtliche Aktivitäten, die zum Satz über die Innenwinkelsumme in Dreiecken führen!
- Entwickeln Sie eine Unterrichtseinheit, in der eine Formel für das Maß eines Innenwinkels in regelmäßigen n-Ecken erarbeitet wird!
Thema 1
- Formulieren und beweisen Sie den Satz des Thales sowie dessen Umkehrung! Hierbei dürfen zugrundeliegende Sätze als bekannt vorausgesetzt werden.
- Erläutern Sie je eine unterrichtliche Aktivität zur Hinführung auf die zentrale Aussage des Satzes des Thales bzw. seiner Umkehrung! Diskutieren Sie hierbei den Einsatz dynamischer Geometriesoftware!
- Entwickeln Sie eine Unterrichtseinheit zum Umkreis von Dreiecken, in der die Lage des Umkreismittelpunkts untersucht wird!
Thema 2
- Erläutern Sie den Begriff "lineare Funktion"!
- Diskutieren Sie zwei unterrichtliche Aktivitäten zur Einführung linearer Funktionen!
- Entwickeln Sie eine Unterrichtseinheit zur Orthogonalität von Graphen linearer Funktionen!
Thema 3
- Erläutern Sie die Begriffe "integrierbar", "bestimmtes Integral" und "Integralfunktion"!
- Erläutern Sie zwei Grundvorstellungen, die Schülerinnen und Schüler zu bestimmten Integralen entwickeln sollen!
- Entwickeln Sie eine Unterrichtseinheit, in der anhand einer Aufgabe zum bestimmten Integral die Kompetenz "Probleme mathematisch lösen" gefördert wird!
Thema 1
- Erläutern Sie das Prinzip von Cavalieri und seine Anwendung im Mathematikunterricht des Gymnasiums!
- Beschreiben und diskutieren Sie drei verschiedene Arten von Körpermodellen! Erläutern Sie dazu jeweils eine unterrichtliche Aktivität bei der Behandlung von geraden Prismen oder Kreiszylindern!
- In einer Unterrichtseinheit soll das Kugelvolumen erarbeitet werden. Formulieren Sie dazu Lernvoraussetzungen und Lernziele! Beschreiben Sie den Unterrichtsverlauf und begründen Sie diesen unter fachdidaktischen Gesichtspunkten!
Thema 2
- Erläutern Sie den Begriff der Monotonie von Funktionen, soweit er für die Schule relevant ist!
- Erläutern Sie zwei unterrichtliche Aktivitäten zur Kompetenz "mathematisch argumentieren" im Themengebiet der Monotonie!
- Entwerfen Sie eine Unterrichtseinheit, in der ein Zusammenhang von Monotonieverhalten und erster Ableitung erarbeitet wird!
Thema 3
- Leiten Sie den Term der Ableitungsfunktion der Sinusfunktion auf Niveau der Sekundarstufe II her! Der Grenzwert \(\lim_{x\to 0}\frac{\sin(x)}{x} = 1\) darf als bekannt vorausgesetzt werden.
- Beschreiben und diskutieren Sie zwei verschiedene unterrichtliche Zugänge zu den Begriffen "Sinus" und "Kosinus"!
- In einer Unterrichtseinheit sollen folgende Zusammanhänge behandelt werden: \( (\sin\alpha)^2 + (\cos\alpha)^2 = 1 \) und \( \cos\alpha = \sin(90°-\alpha) \) . Geben Sie die Lernvoraussetzungen an und nennen Sie Lernziele! Beschreiben Sie einen Stundenverlauf und begründen Sie diesen unter fachdidaktischen Gesichtspunkten!
Thema 1
- Charakterisieren Sie die wichtigsten Vierecksformen in der Sekundarstufe I anhand der Eigenschaft Symmetrie!
- Erläutern Sie zwei unterrichtliche Zugänge zur Flächeninhaltsformel für das Drachenviereck!
- Nennen Sie Lernvoraussetzungen und Lernziele in einer Unterrichtseinheit zur Analyse von Umkreisen an Vierecken! Schildern Sie wesentliche unterrichtliche Schritte und begründen Sie diese unter mathematik-didaktischen Gesichtspunkten!
Thema 2
- Erläutern Sie eine Herleitung der Eulerschen Zahl auf Schulniveau!
- Erläutern Sie jeweils eine Aufgabenstellung zu exponentiellen Wachstumsprozessen, die die Kompetenz "mathematisch modellieren" bzw. "mathematische Darstellungen verwenden" fokussiert!
- Entwickeln Sie eine Unterrichtseinheit, in der Eigenschaften der Umkehrfunktion der natürlichen Exponentialfunktion erarbeitet werden!
Thema 3
- Erläutern Sie den Begriff "irrationale Zahl" und beweisen Sie, dass \(\sqrt{10}\) irrational ist!
- Beschreiben Sie zwei unterrichtliche Aktivitäten zur Lösung der Gleichung \(\sqrt{x^2}-10 = 0\).
- Entwickeln Sie eine Unterrichtseinheit zur näherungsweisen Bestimmung von \(\sqrt{10}\).
THEMA 1
- Stellen Sie aus fachlicher Perspektive dar, wie Formeln für die Oberfläche von geraden Zylindern, geraden Kreiskegeln und Kugeln begründet werden können!
- Erläutern Sie zwei Aufgabenstellungen, mit denen anhand von Oberflächen oder Volumina geometrischer Körper funktionales Denken von Schülerinnen und Schülern gefördert werden kann!
- In einer Unterrichtseinheit sollen Oberflächeninhalte von Quadern bestimmt werden. Nennen Sie Lernvoraussetzungen und Lernziele! Schildern Sie einen möglichen Unterrichtsverlauf und begründen Sie diesen unter fachdidaktischen Gesichtspunkten!
THEMA 2
- Erläutern Sie den Funktionsbegriff und zugehörige Grundvorstellungen!
- Erläutern Sie anhand geeigneter Beispiele der Sekundarstufe II, wie Definitions- und Wertemenge sowie Monotonie und Ableitung von Funktion und zugehöriger Umkehrfunktion zusammenhängen!
- Entwerfen Sie eine Unterrichtseinheit, in der die Ableitung der natürlichen Logarithmusfunktion erarbeitet wird! Die allgemeine Formel zur Bestimmung der Ableitung der Umkehrfunktion darf nicht vorausgesetzt werden!
THEMA 3
- Erläutern Sie die Begriffe "Ähnlichkeitsabbildung" und "Ähnlichkeit ebener Figuren"!
- Entwerfen Sie zwei für den Unterricht geeignete Aufgaben zu Strahlensätzen! Dabei sollen zwei verschiedene prozessbezogene Kompetenzen im Sinne der KMK-Bildungsstandards im Vordergrund stehen! Diskutieren Sie die Eignung der Aufgaben zur Förderung der jeweiligen Kompetenz!
- Skizzieren Sie eine Unterrichtseinheit zur Anwendung des Strahlensatzes an der V-Figur in realitätsbezogenen Kontexten! Geben Sie Lernvoraussetzungen an und nennen Sie Lernziele! Beschreiben Sie einen Stundenverlauf und begründen Sie diesen unter fachdidaktischen Gesichtspunkten!
THEMA 1
1. Erläutern Sie den Begriff "gebrochen-rationale Funktion"!
2. Beschreiben Sie zwei unterrichtliche Aktivitäten zur Untersuchung des Symmetrieverhaltens von Funktionen!
3. Entwickeln sie eine Unterrichtseinheit, in der Funktionen der Form \( f(x) = \frac{a}{x+b}+c\) behandelt werden!
THEMA 2
1. Erläutern Sie die beiden Grundvorstellungen "Tangentensteigung" und "lokale Änderungsrate" zum Ableitungsbegriff!
2. Erläutern Sie die mathematische Kompetenz "Mathematische Darstellungen verwenden" im Rahmen der Leitidee "Funktionaler Zusammenhang" jeweils anhand eines Beispiels der Sekundarstufe I und II!
3. Entwickeln Sie eine Unterrichtseinheit zur Einführung des Ableitungsbegriffs anhand der Tangentenvorstellung!
THEMA 3
1. Erläutern Sie den Begriff Flächeninhalt auf dem Niveau der Unterstufe aus fachlicher Sicht!
2. Die Flächeninhaltsformel für das Trapez kann unterschiedlich interpretiert werden. Erläutern Sie je eine geeignete geometrische Interpretation für \(A = (a+c)\cdot\frac{h}{2} \) bzw. \(A = \frac{(a+c)}{2}\cdot h \).
Nennen Sie dabei auch Lernziele, die mit der Betrachtung dieser verschiedenen Interpretationen verfolgt werden können!
3. Entwickeln Sie eine Unterrichtseinheit zur Herleitung der Flächenformel eines Trapezes!
THEMA 1
1. Formulieren Sie den Sinussatz und den Kosinussatz und beweisen Sie den Kosinussatz!
2. Erläutern Sie die prozessbezogenen Kompetenzen "Mathematisch modellieren" und " Probleme mathematisch lösen" und grenzen Sie sie voneinander ab!
3. In einer Unterrichtseinheit soll mit dem Sinus- oder dem Kosinussatz ein Modellierungsproblem bearbeitet werden. Formulieren Sie dazu Lernvoraussetzungen und Lernziele! Beschreiben Sie den Unterrichtsverlauf und begründen Sie diesen unter fachdidaktischen Gesichtspunkten!
THEMA 2
1. Leiten Sie die Volumenformel eines geraden Kreiszylinders elemtargeometrisch und mit Mitteln der Integralrechnung her!
2. Beschreiben Sie anhand ausgewählter Beispiele zwei unterschiedliche schulische Methoden zur Lösung von Extremwertproblemen mit Nebenbedingungen!
3. In einer Unterrichtseinheit soll unter allen geraden Kreiszylindern mit konstantem Volumen derjenige bestimmt werden, dessen Oberflächeninhalt minimal ist. Erstellen Sie eine Sachanalyse mit einer Lösung dieser Aufgabe und skizzieren sie einen didaktisch begründeten möglichen Unterrichtsverlauf!
THEMA 3
1. Formulieren Sie die Regel zur Ableitung von Potenzfunktionen \( x\mapsto x^n,~n\in\mathbb{N}_0\) ! Diskutieren Sie zwei unterschiedliche Begründungen für diese Regel im Spannungsfeld aus schulischer Zugänglichkeit und fachlicher Stimmigkeit!
2. Schildern Sie drei unterrichtliche Aktivitäten zur Untersuchung von quadratischen Funktionen!
3. Entwickeln Sie eine Unterrichtseinheit, in der die folgende Aufgabe bearbeitet wird:
Eine 2m lange Schnur wird einmal durchschnitten. Das eine Teilstück wird zu einem Quadrat, das andere zu einem gleichseitigen Dreieck gelegt. Wo muss der Schnitt erfolgen, damit der gesamte Flächeninhalt minimal wird?
THEMA 1
1. Erläutern Sie den Begriff "n-te Wurzel einer reellen Zahl" und die Lösungsmengen von Gleichungen der Form \( x^n=a,~n\in\mathbb{N},~a\in\mathbb{R} \)!
2. Beschreiben Sie zwei typische Fehler beim Umgang mit dem Wurzelbegriff! Wie kann man ihnen im Mathematikunterricht begegnen?
3. Entwerfen Sie eine Unterrichtseinheit zur Lösung der Gleichung \( \sqrt{-x}=|x| \).
THEMA 2
1.a ) Formulieren und beweisen Sie den Satz des Pythagoras!
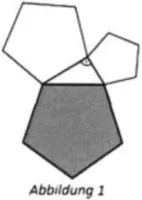
1. b) Zeigen Sie, dass der Satz des Pythagoras auch auf regelmäßige n-Polygone (für ein festes \( n\in\mathbb{N}\) ) über den Seiten eines rechtwinkligen Dreiecks erweitert werden kann (vgl. Abbildung 1)!
Sie dürfen für diese Teilaufgabe verwenden: Sei s die Seitenlänge und n die Anzahl der Seiten eines regelmäßigen Polygons. Der Flächeninhalt dieses n-Polygons kann berechnet werden über \( A_s=s^2\cdot\frac{n}{4\tan(\frac{\pi}{n})} \).
2. Entwerfen Sie zur Leitidee "Raum und Form" zwei Aufgabenstellungen zum "mathematischen Argumentieren"! Erläutern Sie, warum die Kompetenz "Mathematisch argumentieren" im Sinne der Bildungsstandards in diesen Aufgaben angesprochen wird"
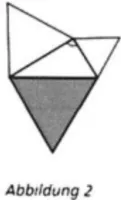
3. Entwickeln Sie eine Unterrichtseinheit, in der gezeigt wird, dass der Satz des Pythagoras auch auf gleichseitige Dreiecke über den Seiten eines
rechtwinkligen Dreiecks (vgl. Abbildung 2) erweitert werden kann!
THEMA 3
1. Formulieren und beweisen Sie die Regel zur partiellen Integration!
2. Beschreiben Sie die Leitidee "Messen" gemäß den Bildungsstandards und stellen Sie einen Zusammenhang zum Integralbegriff her!
3. Entwickeln Sie eine Unterrichtseinheit zum Thema "Flächeninhalt und bestimmtes Integral", in der digitale Medien eingesetzt werden!
THEMA 1
1. Erläutern Sie die Begriffe "Stammfunktion", "Integralfunktion" und "bestimmtes Integral" auf dem Niveau der Sekundarstufe II!
Gehen Sie dabei auch auf Existenz und Eindeutigkeit ein!
2. Erläutern Sie zwei verschiedene (Grund-)Vorstellungen, die Lernende am Ende der Sekundarstufe II mit dem Begriff des bestimmten Integrals verbinden sollen!
Beschreiben und begründen Sie eine Lernaktivität, die den Lernenden ermöglicht, Beziehungen zwischen diesen beiden Vorstellungen herzustellen!
3. In einer Unterrichtseinheit soll der Hauptsatz der Differential- und Integralrechnung erarbeitet und begründet werden. Beschreiben Sie wesentliche unterrichtliche
Schritte und begründen Sie diese unter fachdidaktischen Gesichtspunkten!
THEMA 2
1. Erläutern Sie die Begriffe Prisma, Zylinder, Pyramide und Kegel!
2. Beschreiben und diskutieren Sie drei verschiedene Arten von Körpermodellen!
Verwenden Sie dazu jeweils eine geeignete unterrichtlche Aktivität bei der Behandlung von geraden Prismen und Kreiszylindern!
3. Entwickeln Sie eine Unterrichtseinheit, in der die Volumenformel von geraden Prismen erarbeitet wird!
THEMA 3
1. Erläutern Sie die unterschiedlichen algebraischen Darstellungsformen von quadratischen Funktionen und vergleichen Sie diese bezüglich ihrer Anwendbarkeit in spezifischen Fragestellungen!
2. Entwerfen Sie eine Modellierungsaufgabe zu einem Extremwertproblem (mit Lösungsskizze), die sich in der Mittelstufe unter Rückgriff auf quadratische Funktionen lösen lässt! Erläugern Sie, inwiefern die Kompetenz "Mathematisch modellieren" in dieser Aufgabe angesprochen wird!
3. Entwickeln Sie eine Unterrichtseinheit, in der die Bedeutung des Parameters \( a \) in \( f(x)=a(x-b)^2+c \) erläutert wird!
THEMA 1
1. Erläutern Sie den Begriff der "Ableitung einer reellen Funktion an einer Stelle"!
2. Erläutern Sie unterrichtliche Aktivitäten zu Monotoniekriterien für reelle Funktionen!
3. Entwickeln Sie eine Unterrichtseinheit, in der die Ableitungsfunktion der Funktion \( f(x)=\frac{1}{x^2},~x\in\mathbb{R}\setminus\{0\} \) erarbeitet wird!
THEMA 2
1. Erläutern Sie grundlegende Begriffe und Zusammenhänge der Prozentrechnung!
2. Beschreiben Sie für die Prozentrechnung typische Schülerfehler! Erläutern Sie Möglichkeiten, wie diesen Schwierigkeiten im Unterricht begegnet werden kann!
3. Entwickeln Sie eine Unterrichtseinheit, in der der Prozentbegriff eingeführt wird! Die "Prozentformel" muss dabei noch nicht thematisiert werden.
THEMA 3
1. Begründen Sie die drei binomischen Formeln auf jeweils zwei verschiedene Arten! Benennen Sie dabei jeweils die genutzten fachlichen Grundlagen!
2. Erläutern Sie drei Anwendungen der binomischen Formeln in unterschiedlichen Inhaltsbereichen des Mathematikunterrichts!
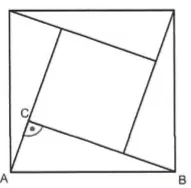
3. Entwickeln Sie eine Unterrichtseinheit zum Satz des Pythagoras! Verwenden Sie in Ihren Ausführungen die nachfolgende Figur:
Thema I
-
Formulieren und beweisen Sie den Hauptsatz der Differential- und Integralrechnung auf dem Niveau der Sekundarstufe II!
-
Im Lehrplan PLUS wird der Begriff der Stammfunktion in der elften, der des Integrals in der zwölften Jahrgangsstufe eingeführt. Erläutern sie, welche Gründe dafür sprechen, den Begriff Stammfunktion deutlich vor der Integralrechnung zu behandeln! Geben sie dazu passende unterrichtliche Aktivitäten an!
-
Entwerfen sie eine Unterrichtseiheit zur Einführung des Begriffs Stammfunktion!
Thema II
Im Lehrplan PLUS für Jahrgangsstufe 10 steht:
"Die Schülerinnen und Schüler [...] bestimmen mithilfe der Monte-Carlo-Methode unter Einsatz eines Tabellenkalkulationsprogramms oder einer anderen geeigneten Software (z. B. unter Verwendung bedingter Anweisungen) einen Näherungswert für die Kreiszahl Pi. Sie vergleichen dieses Verfahren mit einem nicht zufallsbasierten Verfahren zur Bestimmung eines Näherungswerts von Pi, das z. B. auf der Streifenmethode beruht."
- Erläutern Sie, wie mit der Monte-Carlo-Methode ein Näherungswert für Pi gewonnen werden kann! Skizzieren Sie, wie dies mit digitalen Medien umgesetzt werden kann!
- Nennen Sie zunächst zwei nicht-zufallsbasierte Verfahren zur Bestimmung von Näherungswerten für Pi!
Diskutieren Sie dann ausführlich das fachdidaktische Potential von zufallsbasierten und nicht-zufallsbasierten Verfahren zur Bestimmung von Näherungswerten für Pi im Unterricht der Sekundarstufe I! - Entwickeln Sie eine Unterrichtseinheit, in der mit der Monte-Carlo-Methode Näherungswerte für Pi gewonnen werden!
Thema III
- Geben Sie einen Überblick über Möglichkeiten zur Berechnung von unbekannten Winkeln und Längen in geradlinig begrenzten geometrischen Figuren im Mathematikunterricht! Formulieren Sie zwei Sätze der Schulgeometrie, die im Kontext solcher Berechnungen genutzt werden können! Beweisen Sie einen dieser Sätze!
- Erläutern Sie die allgemeine mathematische Kompetenz "Problemlösen"! Gehen sie auch auf Möglichkeiten zur Förderung von Problemlösekompetenzen im Mathematikunterricht ein!
- In einer Unterrichtseinheit sollen Problemlösekomptenzen im Kontext von geometrischen Berechnungsproblemen gefördert werden. Geben Sie Lernvoraussetzungen an und nennen Sie Lernziele! Beschreiben Sie einen Stundenverlauf und begründen Sie diesen unter fachdidaktischen Gesichtspunkten!
Thema I
- Definieren Sie den Begriff "lokales Maximum" einer reellen Funktion! Geben Sie Bedingungen für Extremstellen von reellen Funktionen an! Berücksichtigen Sie dabei notwendige sowie hinreichende Bedingungen! Begründen Sie eine dieser Bedingungen auf dem Niveau der Sekundarstufe II!
- Beschreiben Sie zwei unterschiedliche Strategien zum näherungsweisen Auffinden von Extremstellen reeller Funktionen!
- Entwickeln Sie eine Unterrichtseinheit, in der der Zusammenhang von Extremstellen einer reellen Funktion und dem Verhalten ihrer Ableitungsfunktion erarbeitet werden soll!
Thema II
- Erläutern Sie die Begriffe "Ähnlichkeitsabbildung" und "Ähnlichkeit ebener Figuren"!
- Erläutern Sie zwei für den Unterricht geeignete Vermessungsprobleme, die auf unterschiedlichen Wegen mit Hilfe von Ähnlichkeitsüberlegungen zu lösen sind!
- Entwickeln Sie eine Unterrichtseinheit, in der der Zusammenhang zwischen den Flächeninhalten von zueinander ähnlichen Figuren erarbeitet werden soll!
Thema III
- Erläutern Sie Sinus, Kosinus und Tangens eines Winkels am rechtwinkligen Dreieck!
- Formulieren Sie eine Aufgabe zur Anwendung von "Sinus, Kosinus und Tangens eines Winkels am rechtwinkligen Dreieck" (mit Lösungsskizze), bei der die allgemeine mathematische Kompetenz "Probleme mathematisch lösen" im Sinne der Bildungsstandards für den Mittleren Schulabschluss angesprochen wird! Begründen Sie, warum die Aufgabe gerade diese Kompetenz anspricht!
- Entwickeln Sie eine Unterrichtseinheit zum Sinus am Einheitskreis für die Jahrgangsstufe 10! Geben Sie Lernvoraussetzungen an und nennen Sie Lernziele! Beschreiben Sie einen Stundenverlauf und begründen sie diesen unter fachdidaktischen Gesichtspunkten!
THEMA I
- Erläutern Sie die Ableitung von Exponentialfunktionen. Gehen Sie sowohl auf die Bedeutung der Basis e (Eulersche Zahl) als auch auf allgemeine Basen ein.
- Erläutern Sie zwei verschiedene Grundvorstellungen für den Ableitungsbegriff in der gymnasialen Oberstufe.
- Entwickeln Sie eine Unterrichtseinheit zur Ableitung der allgemeinen Exponentialfunktion \(f(x) = ax\) in der 11. Jahrgangsstufe.
THEMA II
- Formulieren Sie den Satz von der Innenwinkelsumme im Dreieck und beweisen Sie diesen Satz auf zwei verschiedene Arten auf dem Niveau der Sekundarstufe I.
- Entwickeln Sie drei Lernaufgaben zum Themenbereich "Winkelbeziehungen an parallelen Geraden", in denen jeweils eine andere allgemeine mathematische Kompetenz im Sinne der Bildungsstandards für den mittleren Schulabschluss im Vordergrund steht. Begründen Sie Ihre Auswahl.
- Entwickeln Sie eine Unterrichtseinheit, in der der Satz von der Innenwinkelsumme in (konvexen) Polygonen erarbeitet wird.
THEMA III
- Diskutieren Sie zwei schulrelevante Zugänge zum Begriff "Sinus eines Winkels". Erläutern Sie in diesem Zusammenhang Eigenschaften, die jeweils mit diesen Zugängen erarbeitet werden können.
- Diskutieren Sie unterrichtliche Möglichkeiten, wie man die Sinuswerte für 30 Grad und 90 Grad bestimmen kann.
- Entwerfen Sie eine Unterrichtseinheit, in der die Ableitung der Sinusfunktion hergeleitet wird.
THEMA I
- Beschreiben Sie anhand von Beispielen aus der Analysis verschiedene Aspekte des Funktionsbegriffs.
- Erläutern Sie zwei Vorstellungen, die Schülerinnen und Schüler mit der 2. Ableitungsfunktion einer (zweimal differenzierbaren) Funktion verbinden sollen.
- Entwickeln Sie eine Unterrichtseinheit, in der der Begriff des Wendepunktes eingeführt wird.
THEMA II
- Erläutern SIe den Begriff "Parallelität" für Geraden in Ebene und Raum.
- Skizzieren Sie, wie, ausgehend von einer geeigneten Definition, im Unterricht Eigenschaften von Parallelogrammen abgeleitet werden können! Gehen Sie dabei auch auf die Verwendung konkreter Modelle ein.
- Entwickeln Sie eine Unterrichtseinheit, in der verschiedene Möglichkeiten zur Flächeninhaltsberechnung von Rauten thematisiert werden.
THEMA III
- a) Erläutern Sie den Begriff "Wurzel" und stellen Sie dabei einen Zusammenhang zum Potenzbegriff her!
b) Beweisen Sie die Irrationalität von \(\sqrt{2}\) . - Beschreiben Sie anhand aussagekräftiger Beispiele drei typische Schülerfehler im Umgang mit Quadratwurzeln und erläutern Sie deren Ursachen! Beziehen Sie auch Gleichungen oder Funktionen in Ihre Überlegungen mit ein.
- Entwickeln Sie eine Unterrichtseinheit, in der der Begriff "reelle Zahl" eingeführt wird.
Thema I
- Erläutern Sie die Begriffe Exponentialfunktion und Logarithmusfunktion. Berücksichtigen Sie dabei auch Inhalte auf dem Niveau der Sekundarstufe II!
- Erläutern Sie zwei unterrichtliche Zugänge zur Euler’schen Zahl \(e\)!
- In einer Unterrichtsstunde soll die Ableitung der natürlichen Logarithmusfunktion behandelt werden. Formulieren Sie wichtige Lernziele und Lernvoraussetzungen! Beschreiben Sie wesentliche Schritte eines möglichen Unterrichtsverlaufs und begründen Sie das Vorgehen im Unterricht unter fachdidaktischen Gesichtspunkten!
Thema II
- Formulieren Sie den Satz des Pythagoras und beweisen Sie diesen Satz einmal auf Grundlage des Konzepts der Zerlegungs- oder Ergänzungsgleichheit und einmal auf Grundlage des Konzepts der Ähnlichkeit!
- Beschreiben Sie die allgemeine mathematische Kompetenz „Mathematisch argumentieren“ im Sinne der Bildungsstandards für den mittleren Schulabschluss. Illustrieren Sie Ihre Beschreibung anhand von drei Beispielen aus dem Bereich der Geometrie!
- Entwickeln Sie eine Unterrichtseinheit, in der eine Formel für die Länge der Raumdiagonale des Quaders hergeleitet wird!
Thema III
- Erläutern Sie die Begriffe „Kongruenz“ und „Symmetrie“ für ebene Figuren!
- Beschreiben Sie unterrichtliche Aktivitäten zum Symmetriebegriff!
- Entwickeln Sie eine Unterrichtseinheit zur Einführung des „SsW-Satzes“ (Kongruenzsatz für Dreiecke)!
Thema I
- Formulieren und Beweisen Sie den Kosinussatz.
- Beschreiben Sie die allgemeine mathematische Kompetenz "Mathematik modellieren" im Sinne der Bildungsstandards für den mittleren Schulabschluss. Illustrieren Sie Ihre Beschreibung anhand von drei Beispielen aus dem Bereich der Geometrie.
- Entwickeln Sie eine Unterrichtseinheit, in der eine Anwendungsaufgabe zum Kosinussatz behandelt wird.
Thema II
- Erläutern Sie zwei Aspekte oder (Grund-)Vorstellungen, die Schülerinnen und Schüler mit dem Integralbegriff verbinden sollen.
- Beschreiben Sie die Leitidee "Messen" im Sinne der Bildungsstandards anhand des Größenbereichs "Flächeninhalte". Gehen Sie dabei auch auf die Weiterführung in der Sekundarstufe II ein.
- Entwickeln Sie eine Unterrichtseinheit, in der der Begriff "Integralfunktion" eingeführt wird.
Thema III
- Erläutern Sie den Begriff Bernoulli-Kette.
- Erläutern Sie an drei Beispielen Möglichkeiten eines didaktisch sinnvollen Computereinsatzes im Stochastikunterricht.
- Entwerfen Sie eine Unterrichtseinheit zur Binomialverteilung in der Sekundarstufe II.
Thema I
- Erläutern Sie, was man im Kontext von Flächeninhalten unter „Messen“ versteht!
- Erläutern Sie zwei wesentlich verschiedene unterrichtliche Möglichkeiten, im Zusammenhang mit der Behandlung des Flächeninhalts eines Kreises einen Näherungswert für \(\pi\) zu ermitteln!
- In einer Unterrichtseinheit soll der Zusammenhang zwischen Durchmesser und Umfang eines Kreises erarbeitet werden. Nennen Sie Lernvoraussetzungen und Ziele! Begründen Sie wesentliche unterrichtliche Schritte unter fachdidaktischen Gesichtspunkten!
Thema II
- Erläutern Sie den Begriff „Sinusfunktion“, wie er in der Sekundarstufe I verwendet wird! Geben Sie dabei auch auf die Bedeutung der Parameter in der Gleichung der allgemeinen Sinusfunktion \(y=a \sin (b(x+c))+d\) mit \(a>0, b>0,c,d \in \mathbb{R}\) ein!
- Beschreiben Sie zwei Möglichkeiten, die Ableitung der Sinusfunktion im Unterricht zu erarbeiten! Gehen Sie dabei auch auf die nötigen Vorkenntnisse der Schülerinnen und Schüler ein!
- Entwickeln Sie eine Unterrichtseinheit, in der das Modellieren von periodischen Vorgängen im Mittelpunkt steht!
Thema III
- Erläutern Sie die Begriffe „Kongruenzabbildung“ und „Kongruenz von Figuren“ in der ebenen Geometrie!
- Erläutern Sie unterrichtliche Aktivitäten zur Innenwinkelsumme im Dreieck!
- In einer Unterrichtsstunde sollen Eigenschaften von gleichschenkligen Dreiecken erarbeitet und begründet werden. Geben Sie Lernvoraussetzungen an und nennen Sie Lernziele! Beschreiben Sie einen Stundenverlauf und begründen Sie diesen unter fachdidaktischen Gesichtspunkten!
Thema I
- Erläutern Sie die Darstellung rationaler Zahlen als "gewöhnlicher Bruch" und "Dezimalbruch"!
- Beschreiben Sie drei verschiedene typische Fehler von Schülerinnen und Schülern beim Rechnen mit gewöhnlichen Brüchen und erläutern Sie mögliche Ursachen!
- Entwickeln Sie eine Unterrichtseinheit zur Multiplikation von Dezimalbrüchen!
Thema II
- Geben Sie einen Überblick über den Themenbereich "Sinus und Kosinus" im Mathematikunterricht der Sekundarstufe I!
- Erläutern Sie an Beispielen, inwiefern die Nutzung digitaler Medien einen fachdidaktischen Mehrwert im Mathematikunterricht bieten kann!
- Entwickeln Sie eine Unterrichtseinheit im Themenbereich „Sinus und Kosinus“, bei der digitale Medien genutzt werden!
Thema III
- Erläutern Sie die Leitidee "Funktionaler Zusammenhang" gemäß den Bildungsstandards!
- Erläutern Sie, was Schülerinnen und Schüler am Ende der Sekundarstufe II über die Potenzfunktionen \(f\) mit \( f (x) = x^n, D= \mathbb{R} , n \in \mathbb{N}\) wissen sollten!
- Entwickeln Sie eine Unterrichtseinheit, in der die Ableitung der Potenzfunktion \( f\) mit \(f (x) = x^3,\ D= \mathbb{R}\) behandelt wird!
Thema I
- Erläutern Sie das Prinzip von Cavalieri und seine Anwendung im Mathematikunterricht des Gymnasiums!
- Geben Sie einen Überblick, bei welchen Themengebieten Grenzwertprozesse im Mathematikunterricht der Sekundarstufe 1 eine Rolle spielen!
- Skizzieren Sie eine Unterrichtssequenz zur Ermittlung des Volumens und der Oberfläche der Kugel!
Thema II
- Formulieren und beweisen Sie die Ableitungsregel für die Funktion mit der Gleichung \(f(x)=x^n \text{ mit }x \in\mathbb{R} \text{ und }n \in \mathbb{N}.\)
- Erläutern Sie wesentliche Schritte in der Entwicklung des Potenzbegriffs im Verlauf des Mathematikunterrichts am Gymnasium!
- In einer Unterrichtseinheit sollen Zusammenhänge zwischen den Graphen einer Funktion, ihrer Ableitungsfunktion und einer Stammfunktion behandelt werden. Wählen Sie dazu ein geeignetes Beispiel und erläutern Sie wesentliche unterrichtliche Schritte unter fachdidaktischen Gesichtspunkten!
Thema III
- Skizzieren Sie zwei didaktische Konzepte zur Erarbeitung des Bereichs der Bruchzahlen! Erläutern Sie Stärken und Schwächen der Konzepte für den Mathematikunterricht!
- Diskutieren Sie verschiedene Möglichkeiten zum Größenvergleich von Brüchen! Gehen Sie dabei sowohl auf gewöhnliche Brüche als auch auf Dezimalbrüche ein!
- Entwickeln Sie eine Unterrichtseinheit zum "Kürzen und Erweitern von gewöhnlichen Brüchen"! Formulieren Sie geeignete Aufgabenstellungen für diese Unterrichtseinheit und begründen Sie Ihre Wahl unter fachdidaktischen Gesichtspunkten!
Thema I
- Erläutern Sie die Begriffe "Ableitungsfunktion" und "Integralfunktion" sowie Beziehungen zwischen diesen Begriffen!
- Erläutern Sie je zwei grundlegende Vorstellungen, die Schülerinnen und Schüler zum Ableitungsbegriff sowie zum Integralbegriff entwickeln sollten!
- Entwickeln Sie eine Unterrichtseinheit zum Thema "Ableitung von Potenzfunktionen"!
Thema II
- Formulieren Sie den Höhensatz in Worten und in Formelschreibweise und beweisen Sie diesen Satz auf zwei verschiedene Arten!
- Erläutern Sie Gründe dafür, Beweisen/Argumentieren im Mathematikunterricht zu behandeln! Geben Sie jeweils ein Beispiel an, wo im Geometrieunterricht anschaulich und wo eher formal bewiesen/argumentiert werden kann!
- Nennen Sie Lernvoraussetzungen und Lernziele einer Unterrichtseinheit zu Anwendungen des Höhensatzes! Schildern Sie jeweils wesentliche unterrichtliche Schritte und begründen Sie diese unter mathematikdidaktischen Gesichtspunkten!
Thema III
- Erläutern Sie mit Hilfe aussagekräftiger Beispiele die Begriffe "rational", "irrational", "algebraisch" und "transzendent" für Zahlen und stellen Sie Zusammenhänge zwischen diesen Begriffen dar!
- Beschreiben und diskutieren Sie zwei Verfahren zur näherungsweisen Bestimmung der Kreiszahl π.
- In einer Unterrichtseinheit in der Jahrgangsstufe 8 soll die Kreiszahl π eingeführt werden. Skizzieren Sie einen möglichen Unterrichtsverlauf und begründen Sie wesentliche Schritte aus didaktischer Sicht!
Thema I
- Beschreiben Sie die Streifenmethode zur Bestimmung von Integralen und führen Sie diese am Beispiel von \(\int_0^1 x^2dx\) durch!
- Erläutern Sie verschiedene Vorstellungen, die bei der Behandlung des Integralbegriffs ausgebildet werden sollten!
- Entwickeln Sie eine Unterrichtseinheit zur Berechnung von Flächeninhalten zwischen zwei Funktionsgraphen!
Thema II
-
- Formulieren und begründen Sie die Regel für die Ableitung von verketteten Funktionen auf Niveau der Sekundarstufe II!
- Verwenden Sie die Kettenregel, um allgemein die Ableitung der Umkehrfunktion einer Funktion zu bestimmen!
- Erläutern Sie zwei Zugänge zur natürlichen Logartithmus-Funktion!
- Entwerfen Sie eine Unterrichtseinheit zur Einführung der natürlichen Logarithmus-Funktion!
Thema III
- Formulieren und beweisen Sie den Satz des Thales sowie seine Umkehrung! Geben Sie eine im Mathematikunterricht des Gymnasiums zugängliche Verallgemeinerung des Satzes von Thales an!
- Erläutern Sie je eine unterrichtliche Aktivität, die es Lernenden ermöglichet, die Aussage des Satzes von Thales bzw. seiner Umkehrung selbständig zu entdecken!
- In einer Unterrichtseinheit sollen Anwendungen des Sates von Thales sowie seiner Umkehrung behandelt werden. Beide Aussagen sind bereits bekannt. Ein Ziel soll dabei sein, die beiden Aussagen zu kontrastieren.
Formulieren Sie geeignete Aufgabenstellungen für diese Unterrichtseinheit und begründen Sie Ihre Wahl unter fachdidaktischen Gesichtspunkten!
Thema I
- Erläutern Sie, welche Kenntnisse und Fähigkeiten Schülerinnen und Schüler am Ende der Jahrgangsstufe 12 bezüglich Funktionen des Typs \(f:x\mapsto a^x \quad (a\in \mathbb{R}^+)\)besitzen sollten!
- Entwerfen Sie eine Aufgabe, die eine Anwendung einer Exponentialfunktion aufzeigt (mit Lösungsskizze)! Erläutern Sie dabei auch Lernziele, die mit dieser Aufgabe verfolgt werden können.
- Entwickeln Sie eine Unterrichtseinheit, in deren Mittelpunkt die Funktion \(f:x\mapsto e^{-x^2}\)und ihre Ableitungsfunktion stehen!
Thema II
- Erläutern Sie die Begriffe „arithmetisches Mittel” und „Standardabweichung”
- Erläutern Sie unterrichtliche Aktivitäten zum Thema „statistische Diagramme”!
- Entwerfen Sie eine Unterrichtseinheit zum empirischen Gesetz der großen Zahlen in der gymnasialen Unterstufe!
Thema III
- Erläutern Sie die Begriffe „Ähnlichkeitsabbildung” und „Ähnlichkeit ebener Figuren”!
- Beschreiben Sie zwei thematisch verschiedene innermathematische Problemstellungen, in denen der Ähnlichkeitsbegriff zur Anwendung kommt!
- Entwicklen Sie eine Unterrichtseinheit zur Modellierung einer außermathematischen Situation mit Hilfe des Ähnlichkeitsbegriffs!
Thema I
- Erläutern Sie die Begriffe "Exponentialfunktion" und "Logarithmusfunktion"!
- Beschreiben Sie unterrichtliche Lösungsstrategien für die Gleichung.
- Entwickeln Sie eine Unterrichtseinheit, in der Unterschiede zwischen linearen Funktionen und Exponentialfunktionen herausgearbeitet werden!
Thema II
- Beschreiben Sie mit Hilfe von Beispielen die zwei Pfadregeln der Wahrscheinlichkeitsrechnung!
- Diskutieren Sie an einem typischen Beispiel die Anwendung von Baumdiagrammen und Wahrscheinlichkeitstafeln (Vier-Felder-Tafeln) zur Berechnung bedingter Wahrscheinlichkeiten!
- Entwickeln Sie eine Unterrichtseinheit zum "Ziegenproblem" ("Drei-Türen-Problem")!
Thema III
- Formulieren und beweisen Sie den Satz des Thales und seine Umkehrung!
- Formulieren Sie eine Aufgabe zum Inhaltsbereich "Satz des Thales" (mit Lösungsskizze), bei der mindestens eine allgemeine mathematische Kompetenz im Sinne der Bildungsstandards für den Mittleren Schulabschluss angesprochen wird! Begründen Sie diesen Zusammenhang zwischen der Aufgabe und den Bildungsstandards!
- In der Jahrgangsstufe 7 soll der "Satz des Thales" erarbeitet werden. Nennen Sie wichtige Lernziele! Beschreiben Sie wesentliche Schritte eines möglichen Unterrichtsverlaufs und begründen Sie das Vorgehen im Unterricht unter fachdidaktischen Gesichtspunkten!
Thema I
- Charaktersieren Sie die wichtigsten Vierecksformen durch die Eigenschaft der Symmetrie!
- Erläutern Sie unterrichtliche Zugänge zur Flächeninhaltsformel für das Trapez!
- Nennen Sie Lernvoraussetzungen und Lernziele einer Unterrichtseinheit zur Einführung der Flächeninhaltsformel des Trapezes! Schildern Sie wesentliche unterrichtliche Schritte und begründen Sie diese unter mathematikdidaktischen Gesichtspunkten!
Thema II
- Formulieren und begründen Sie den Hauptsatz der Differential- und Integralrechnung für stetige Funktionen auf dem Niveau der gymnasialen Oberstufe!
- Erläutern Sie zwei verschiedene Möglichkeiten, das bestimmte Integral im Unterricht einzuführen und gehen Sie jeweils auf Vor- und Nachteile an!
- Entwickeln Sie eine Unterrichtseinheit, in deren Zentrum die Behandlung einer anwendungsbezogenen Problemstellung unter Einsatz der Integralrechnung steht!
Thema III
- Beschreiben Sie die in den Bildungsstandards verankerte mathematische Kompetenz "Modellieren"! Gehen Sie dabei auf Abstufungen in der Komplexität der Modellierungsanforderungen ein.
- Erläutern Sie ein fachdidaktisches Modell für die Bearbeitung von Modellierungsproblemen ("Modellierungskreislauf")! Gehen Sie dabei auch auf mögliche Probleme und Fehler von Lernenden ein!
-
- Geben Sie eine zur Förderung der Modellierungskompetenz geeignete Aufgabe aus dem Bereich "lineare Funktionen" an und begründen Sie Ihre Entscheidung!
- Erläutern Sie zwei Maßnahmen zur Förderung von Modellierungskompetenz!
Thema I
- Erläutern Sie eine mathematische Herleitung der Volumenformel für Pyramiden!
- Geben Sie einen Überblick über die Entwicklung des Volumenbegriffs am Gymnasium!
- Betrachtet wird folgende Aufgabe für die 11. Jahrgangsstufe: "Bei einem Kegel soll die Mantellinie 10 cm lang sein. Wie müssen der Grundkreisradius und die Höhe gewählt werden, damit der Kegel maximales Volumen hat?"
- Stellen Sie einen Term auf, der die Abhängigkeit des Volumens vom Grundkreisradius angibt!
- Nennen Sie drei zentrale Lernziele, die mit dieser Aufgabe verfolgt werden können!
- Welche Schwierigkeiten der Schülerinnen und Schüler erwarten Sie in Bezug auf diese Lernziele? Geben Sie jeweils Unterstützungsmöglichkeiten durch die Lehrkraft an!
Thema II
- Beschreiben Sie zwei Möglichkeiten zur Herleitung der Quotientenregel bei der Ableitung von Funktionen! (Die Kenntnis der Produktregel kann vorausgesetzt werden.)
- Erläutern Sie anhand eines Beispiels, wie der Zusammenhang zwischen Ableitung, Funktion und Stammfunktion im Unterricht behandelt werden kann. Gehen Sie dabei sowohl auf graphische als auch auf formal-symbolische Darstellungen ein!
- Entwickeln Sie eine Unterrichtseinheit zu folgender Aufgabe: "Aus einem DIN-A4-Blatt soll eine nach oben geöffnete quaderförmige Schachtel entstehen, indem man in den vier Ecken quadratische Stücke der Seitenlänge s abschneidet und entsprechende Rechtecke nach oben faltet. Für welchen Wert von s wird das Volumen der Schachtel maximal?"
Thema III
- Erläutern Sie anhand von drei unterschiedlichen Definitionen den Begriff der Parallelität zweier Geraden in der ebenen Euklidischen Geometrie!
- Diskutieren Sie zwei Zugänge zum Begriff der Parallelität für den Unterricht. Machen Sie dabei deutlich, auf welchen unterschiedlichen mathematischen Definitionen die Zugänge beruhen!
- In einer Unterrichtsstunde soll die Formel für den Flächeninhalt des Parallelogramms hergeleitet werden.
- Formulieren Sie drei zentrale kognitive Lernziele für die Unterrichtsstunde
- Diskutieren Sie zwei unterschiedliche didaktische Zugänge zur Herleitung der Formel! Gehen Sie dabei auf relevantes Vorwissen und mögliche Schwierigkeiten er Schülerinnen und Schüler ein!
- Formulieren Sie eine Aufgabe zum Flächeninhalt des Parallelogramms, bei der mathematisches Argumentieren gefordert ist, und begründen Sie Ihre Wahl!
Thema I
- Formulieren Sie den Satz des Pythagoras und zwei unterschiedliche Beweisvarianten. Diskutieren Sie diese Beweise hinsichtlich ihrer Eignung für den Unterricht!
- Erläutern Sie eine innermathematische Anwendung und eine Verallgemeinerung des Satzes des Pythagoras!
- Skizzieren Sie eine Unterrichtssequenz zur "Satzgruppe des Pythagoras". Begründen Sie die Auswahl der Inhalte sowie Ihre Vorgehensweise!
Thema II
- Erläutern Sie den Begriff der Ableitung unter inner- und außermathematischen Gesichtspunkten!
- Diskutieren Sie zwei unterrichtliche Begründungen für die Ableitungsregel der Potenzfunktion , unter didaktischen Gesichtspunkten!
- Entwerfen Sie eine Unterrichtseinheit zur Einführung des Begriffs "Wendepunkt"!
Thema III
- Skizzieren Sie ein Iterationsverfahren zur Ermittlung eines Näherungswerts für π!
- Erläutern Sie unterrichtliche Aktivitäten, anhand derer die Schülerinnen und Schüler die Proportionalität zwischen Umfang und Radius eines Kreises selbst entdecken können! Gehen Sie auch auf Lernvoraussetzungen ein!
- In der 10. Jahrgangsstufe wird das Kugelvolumen behandelt.
- Beschreiben Sie ein realitätsnahes Problem, bei dessen Modellierung das Kugelvolumen gebraucht wird!
- Erläutern Sie Schritte, die ausgehend von konkreten Erfahrungen zum Zusammenhang zwischen Radius und Volumen von Kugeln führen!
- Stellen Sie die Herleitung der Formel für das Kugelvolumen über das Prinzip von Cavalieri dar!
Thema I
- Erläutern Sie das Prinzip des Messens von Längen, Flächeninhalten und Volumina!
- Beschreiben Sie zwei verschiedene Möglichkeiten zur Herleitung der Flächeninhaltsformel eines Dreiecks! Diskutieren Sie dabei unter didaktischen Gesichtspunkten Vor- und Nachteile der Zugänge!
- In einer Unterrichtsstunde in Jahrgangsstufe 7 soll die Grundfläche des Nürnberger Stadions (siehe Abbildung) näherungsweise bestimmt werden!
- Skizzieren Sie eine Musterlösung!
- Erläutern Sie Ziele dieser Stunde! Gehen Sie dabei auch auf die Bildungsstandards ein!
- Welche Schwierigkeiten erwarten Sie?
(Satellitenbild mit Maßstab über http://www.geodaten.bayern.de/BayernViewer2.0)
Thema II
- Erläutern Sie die Begriffe "Integral" und "Integralfunktion"!
- Beschreiben und diskutieren Sie unterrichtliche Zugänge zum Integralbegriff!
- Entwickeln Sie eine Unterrichtseinheit, in der das Verständnis des Hauptsatzes der Differential- und Integralrechnung (HDI) gefördert werden soll!
Thema III
- Erläutern Sie zwei verschiedene Konzepte zur Behandlung der Bruchrechnung!
- Schildern Sie, wie man Schülern die Bedeutung des Dividierens durch einen Bruch in einer Sachsituation anschaulich klar machen kann! Erläutern Sie zwei Möglichkeiten, wie man die Rechenregel "Durch einen Bruch wird dividiert, indem man mit dem Kehrbruch multipliziert" schülergerecht herleiten kann!
- Entwickeln und erläutern Sie ein Schülerarbeitsblatt für eine Unterrichtsstunde, in der die Schüler die Addition von gemeinen Brüchen kennenlernen sollen! Dabei soll insbesondere Wert darauf gelegt werden, dass die Schüler die Möglichkeit haben, Rechenregel zum Addieren von gleichnamigen und ungleichnamigen Brüchen selbst zu entdecken.
Thema I
- Erläutern Sie den Begriff "Pyramide"!
- Beschreiben und diskutieren Sie verschiedene Methoden für die Bestimmung des Volumens von Pyramiden!
- Beschreiben Sie Aufgabenstellungen zum Thema "Pyramide" in der 9.Jahrgangsstufe, mit denen das räumliche Vorstellungsvermögen der Schüler gefördert werden soll!
Thema II
- Erläutern Sie Aufgabenstellungen und Aktivitäten für die Unter- und Mittelstufe, bei denen Extremwertprobleme vorkommen!
- Folgende Aufgabenstellung soll im Unterricht der Oberstufe bearbeitet werden: "Unter den Zylindern mit dem Volumen 1 Liter ist derjenige gesucht, der kleinste Oberfläche hat." Lösen Sie diese Aufgabe! Beschreiben Sie wesentliche unterrichtliche Schritte unter didaktischen Gesichtspunkten!
- Aus einem DIN-A4-Blatt wird ein Zylindermantel gerollt. Ein weiteres Blatt wird der Länge nach halbiert, zu einem rechteckigen, doppelt so langen Streifen zusammengeklebt und ebenfalls zum Zylindermantel mit halber Höhe geformt. Die Halbierung und Verlängerung der Streifen wird schrittweise fortgesetzt! Wie entwickeln sich die Volumina der zu Zylindern ergänzten Körper? Geben Sie einen Term an! Diskutieren Sie die Eignung dieser Aufgabe für den Unterricht!
Thema III
- Erläutern Sie den Begriff der Exponentialfunktion! Gehen Sie dabei auch auf Eigenschaften des Graphen ein!
-
- Erläutern Sie, welche fachlichen Voraussetzungen Schüler zur Einführung der Exponentialfunktion in Jahrgangsstufe 10 mitbringen sollten!
- Wie können Sie im Unterricht die üblichen Einschränkungen für den Parameter b begründen?
- Beschreiben Sie einen außermathematischen Sachverhalt, der zur Einführung der Exponentialfunktion geeignet ist! Welche Schwerpunkte würden Sie bei der Bearbeitung dieses Sachverhalts im Unterricht legen? Begründen Sie ihre Entscheidungen!
Thema I
- Erläutern und diskutieren Sie verschiedene unterrichtsgemäße Deutungen der Ableitung einer reellen Funktion an einer Stelle!
- Zeigen Sie auf, mit welchen Themen des vorausgehenden Unterrichts am Gymnasium diese Deutungen jeweils in Beziehung stehen!
- Entwickeln Sie eine Unterrichtseinheit zum Thema "Lokale Extrema einer Funktion"!
Thema II
- Geben Sie zwei unterschiedliche, für den Unterricht geeignete Aufgabenbeispiele zu den Strahlensätzen an! Erläutern Sie die Unterschiede anhand der Lösungen!
- Ein Schüler stellt folgende Frage: "Warum erscheint auf dem Display eines Kopierers beim Verkleinern bzw. Vergrößern nicht 50% oder 200%, sondern 71% bzw. 141%?" Erläutern Sie didaktische Möglichkeiten der Behandlung dieser Schülerfrage! Welche Ziele können damit erreicht werden?
- Formulieren Sie einen Beweis für den Kathetensatz! Diskutieren Sie diesen Beweis unter didaktischen Geschichtspunkten!
Thema III
- Erläutern Sie den Themenkreis "Symmetrie von Funktionsgraphen" unter fachlichen und didaktischen Gesichtspunkten!
- Diskutieren Sie Vor- und Nachteile von "traditioneller" Kurvendiskussion im Analysisunterricht!
- Perspektiven zur Öffnung des Analysisunterricht könnten u.a. sein:
- Kluge Nutzung neuer Technologien,
- Einbeziehung von Anwendungskontexten,
- veränderte Aufgabenkultur.
Entwickeln und erläutern Sie eine Beispielaufgabe aus dem Bereich Analysis, bei der eine Öffnung des Analysisunterrichts sichtbar wird!
Thema I
- a) Nennen Sie die Regeln für die Ableitung von Summen, Produkten und Quotienten von Funktionen und begründen Sie zwei dieser Regeln auf dem Niveau der Sekundarstufe II.
b) Geben Sie ein Aufgabenbeispiel, bei dem mindestens eine der genannten Ableitungsregeln nützlich ist. Erläutern Sie die Lösung unter didaktischen Gesichtspunkten. - Zeigen Sie an einem innermathematischen Problem, welche Bedeutung die Ableitung bei der Untersuchung von Funktionen hat.
- Erläutern Sie didaktische Ziele, die mit der Behandlung der Ableitung von Sinus- und Kosinusfunktion verbunden werden können.
Thema II
- Erläutern Sie die Themenkreise „Sinus und Kosinus im rechtwinkligen Dreieck“ und „Sinus und Kosinus am Einheitskreis“ unter fachlichen und didaktischen Gesichtspunkten.
- Erläutern Sie den Begriff der Projektarbeit im Mathematikunterricht und gehen Sie dabei insbesondere auf damit verbundene Ziele ein.
- Konzipieren Sie ein Projekt im Mathematikunterricht, in dem die Schüler den Nutzen der Trigonometrie bei Vermessungsproblemen in der Umwelt kennen lernen.
Thema III
- Erläutern Sie die Begriffe „Elementarereignis“, „Ergebnisraum“ und „Laplace-Wahrscheinlichkeit“.
- Diskutieren Sie Ziele des Stochastikunterrichts am Gymnasium.
- Entwerfen Sie eine Unterrichtseinheit zum Arbeiten mit Laplace-Wahrscheinlichkeiten in der Mittelstufe des Gymnasiums.
Thema I
- Beschreiben Sie verschiedene Methoden zum Lösen von Extremwertaufgaben. Denken Sie dabei insbesondere an formale, graphische oder numerische Lösungen.
- Erörtern Sie inner- und außermathematische Situationen, die im Analysisunterricht auf Extremwertaufgaben führen können, unter didaktischen Gesichtspunkten.
- Im Unterricht soll folgende Aufgabe behandelt werden:
„Eine Firma stellt Verpackungen für Getränke her. Sie erhält den Auftrag, für einen Limonadenhersteller eine Packung von 1 Liter zu entwickeln.“
Beschreiben Sie einen möglichen Unterrichtsverlauf und begründen Sie wesentliche Schritte aus didaktischer Sicht.
Lösungshinweise
Thema II
- Erläutern Sie die so genannten Strahlensätze und ihre Umkehrbarkeit.
- a) Diskutieren Sie verschiedene Repräsentationsformen für die Strahlensätze im Unterricht.
b) Zeigen Sie Beziehungen der Strahlensätze zu anderen Themen des Geometrieunterrichts am Gymnasium auf. - Zeigen Sie, wie im Unterricht eine realitätsbezogene Aufgabe mit Hilfe der Strahlensätze bearbeitet werden kann. Geben Sie fachdidaktische Begründungen.
Thema III
- Beschreiben Sie die in den Bildungsstandards für den mittleren Schulabschluss verankerte Kompetenz „mathematisches Argumentieren“. Gehen Sie dabei auf unterschiedliche Anforderungsbereiche ein.
- Beschreiben Sie eine unterrichtliche Situation, die geeignet ist, bereits in Jahrgangsstufe 5 oder 6 mathematisches Argumentieren zu üben.
- Erläutern Sie ein Beispiel für schülergerechtes Beweisen in den Jahrgangsstufen 7 bis 10.
Lösungshinweise