FracVisET: Untersuchung von Visualisierungen für Brüche mit Eye-Tracking
Bei FracVisET (Investigating Fraction Visualizations using Eye Tracking) handelt es sich um ein Forschungsprojekt an der Schnittstelle von Psychologie und Mathematikdidaktik, welches unter anderem Eye-Tracking verwendet, um kognitive Prozesse bei der Verarbeitung von Bruchvisualisierungen zu untersuchen.
Viele Lernende tun sich schwer damit, Brüche richtig zu verstehen – vor allem, wenn es darum geht, ihren Zahlenwert einzuschätzen. Ein Grund dafür ist, dass Brüche anders funktionieren als natürliche Zahlen. Das Denken ist oft stark vom sogannten Natural Number Bias geprägt – also der Tendenz, Brüche wie natürliche Zahlen zu behandeln.
In unserem Forschungsprojekt untersuchen wir mithilfe von Bruchstreifen (schmale, rechteckige Diagramme; siehe Abbildung unten), wie Kinder und Erwachsene Brüche visuell vergleichen. Uns interessiert besonders, wie sich unterschiedliche Darstellungsformen auf die kognitive Verarbeitung auswirken. Wir vergleichen dabei zwei Arten von Bruchstreifen:
- Kontinuierliche Bruchstreifen, bei denen der Bruch als durchgehender Streifen ohne Unterteilungen gezeigt wird (siehe rechte Seite der Abbildung),
- und diskretisierte Bruchstreifen, bei denen der Streifen in gleiche Abschnitte unterteilt ist, die man zählen kann (siehe linke Seite der Abbildung).
Um zu verstehen, wie Menschen beim visuellen Vergleichen von Bruchstreifen vorgehen, nutzen wir die Methode des Eye-Tracking. Dabei zeichnen wir auf, wohin die Teilnehmenden beim Lösen der Aufgaben schauen. Besonders aufschlussreich sind sogenannte Scanpaths, die zeigen, wie sich die Augen bewegen (siehe Abbildung unten).
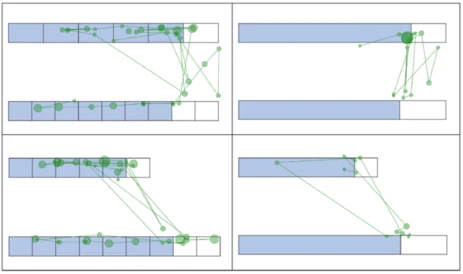
Unsere bisherigen Ergebnisse zeigen:
- Sowohl Kinder als auch Erwachsene erzielen höhere Lösungsraten und sind schneller, wenn sie kontinuierliche Visualisierungen vergleichen.
- Sie nutzen bei kontinuierlichen Visualisierungen seltener ineffiziente Zählstrategien, was darauf hinweist, dass sie die Brüche eher ganzheitlich erfassen statt zu zählen.
- Einige leistungsstarke Kinder zählen trotzdem. Sie sind mit dieser Strategie zwar langsamer, haben aber hohe Lösungsraten.
- Leistungsschwache Kinder neigen dazu, die absoluten Längen der markierten Bereiche statt der Anteile zu vergleichen. Diese Strategie kann zu falschen Lösungen führen und deutet auf ein mangelndes Verständnis von Brüchen hin.
- Eine Analyse von Schulbüchern zeigt: Obwohl kontinuierliche Visualisierungen hilfreich sein könnten, kommen sie dort kaum vor.
Diese Erkenntnisse machen deutlich: Die Art, wie Brüche dargestellt werden, beeinflusst, wie sie kognitiv verarbeitet werden.
Darum ist es wichtig, beim Bruchlernen nicht nur auf die richtige Aufgabenauswahl, sondern auch auf eine didaktisch sinnvolle Gestaltung der Visualisierungen zu achten. Unser Projekt liefert erste Hinweise für die Entwicklung von Unterrichtsmaterialien und digitalen Lernangeboten, die das Verständnis von Brüchen gezielt fördern.
Projektbezogene Publikationen und Präsentationen
Obersteiner, A., Schwarzmeier, S., Alibali, M. W., & Marupudi, V. (2022). Adults' eye movements when comparing discretized or continuous fraction visualizations. In C. Fernández, S. Llinares, A. Gutiérrez, & N. Planas (Hrsg.), Proceedings of the 45th Conference of the International Group for the Psychology of Mathematics Education (Vol. 4, S. 384). PME.
Schwarzmeier, S., Obersteiner, A., Alibali, M. W., & Marupudi, V. (2023). Diskretisierte und kontinuierliche Visualisierungen von Brüchen: Eine Eye-Tracking Studie mit Erwachsenen. In IDMI-Primar Goethe-Universität Frankfurt (Hrsg.), Beiträge zum Mathematikunterricht 2022: 56. Jahrestagung der Gesellschaft für Didaktik der Mathematik. WTM. DOI: 10.37626/GA9783959872089.0
Schwarzmeier, S., Obersteiner, A., Alibali, M. W., & Marupudi, V. (2023). Comparing Continuous and Discretized Tape Diagrams of Fractions: An Eye-Tracking Study with Adults. 20th Biennial EARLI Conference.
Schwarzmeier, S., Obersteiner, A., Alibali, M. W., & Marupudi, V. (2023). Why Continuous Tape Diagrams of Fractions are Easier to Process than Discretized ones: Evidence from Adults’ and Children’s Eye-Movements. WOG 2023.
Schwarzmeier, S., Obersteiner, A., Alibali, M. W., & Marupudi, V. (2024). How do people compare visualizations of fraction magnitudes? Evidence from adults’ and children’s eye movements with continuous and discretized tape diagrams. The Journal of Mathematical Behavior, 75, 101160. DOI: 10.1016/j.jmathb.2024.101160
Schwarzmeier, S., & Obersteiner, A. (2024). Is Students’ Ability of Visually Comparing Fraction Magnitudes Related to Their General Fraction Knowledge? An Eye-Tracking Study. MCLS Conference.
Schwarzmeier, S., Kober, A., & Obersteiner, A. (2024). Visualisierungen von Brüchen in Schulbüchern: Kontinuierlich, diskretisiert oder diskret? In P. Ebers, F. Rösken, B. Barzel, A. Büchter, F. Schacht & P. Scherer (Hrsg.), Beiträge zum Mathematikunterricht 2024. 57. Jahrestagung der Gesellschaft für Didaktik der Mathematik. WTM. DOI: 10.37626/GA9783959872782.0
Schwarzmeier, S., & Obersteiner, A. (2025). Is counting a bad idea? Complex relations among children’s fraction knowledge, eye movements, and performance in visual fraction comparisons. Journal of Experimental Child Psychology, 252, 106181. DOI: 10.1016/j.jecp.2024.106181
Schwarzmeier, S., & Obersteiner, A. (2025). Visualisierungen von Brüchen in Schulbüchern: Diskret, diskretisiert oder kontinuierlich? GEBF-Tagung.